Here's What You Need to Know (and Dr. Fauci Won't Tell You) About Herd Immunity

Warning: There’s gonna be math.

There’s a long explanation below, but if you don’t want to go through the whole thing, here’s the conclusion up front:

First, people aren’t using the term “herd immunity” correctly. The herd immunity threshold is the percentage of a population that must be immune to an infection to stop an epidemic. Herd immunity doesn’t mean that there will be no new cases; it means that each new case will infect fewer than one new case.

But second, once a population reaches herd immunity, the number of new cases will drop, and drop rapidly.

The herd immunity threshold.

The herd immunity threshold can be computed using a somewhat artificial number R₀ — the basic reproduction number. Details of the definition, how it’s computed, and why it’s a bit artificial are below, but the main use of R₀ is that the herd immunity threshold is reached when 1-(1/R₀) of a population is immune. (It’s usually expressed as a percentage, so multiply that number by 100.)

The best estimates of the R₀ for SARS-CoV-2 now put it between 2 and 3, and seem to average around 2.6 (but your mileage may vary, and those numbers are recomputed regularly.)

What this means is that herd immunity will be reached for COVID when the proportion of people who are immune is somewhere between 50 and 67 percent, with the average estimate being around  62 percent. (And don’t forget that both people who have been vaccinated and people who have had COVID and recovered are very probably immune. No matter what famous TV immunologist Stephen Colbert says.)

In today’s news, CBS reports that half of American adults have been vaccinated. The CDC reports that nearly two-thirds of Americans have had at least one vaccination shot, which conveys at least partial immunity, and there have been roughly 33 million reported cases. Total that up against 330 million people, and that comes out in the close neighborhood of 50 percent of the U.S. population should now be immune.

In other words, the U.S. has very probably passed the herd immunity threshold.

That doesn’t mean that if you haven’t had it or been vaccinated you can ignore it. You’re less likely to get it now, but there’s still a real chance you will.

But if we’ve reached herd immunity, then we expect the number of new cases to fall, and in fact (CDC again) the number of new COVID cases in the U.S. is dropping rapidly.

In other words, the epidemic is over.

Now the math.

Imagine you have a new Mars colony with 1,000 residents, and one resident is infected with a new coronavirus which we’ll name MARS-30. We’ll make some basic assumptions:

• Everyone who has not had the virus is susceptible to catching it
• A susceptible exposed person has about a two-thirds chance of being infected
• Once you catch it, the course of the infection lasts for five days, after which you’re no longer susceptible — you’ve recovered. (Or you die, but you still can’t catch it again. I’m a softie; in my hypothetical colony everyone recovers)
• Exactly one person has the infection at time 0. Here’s how the infection spreads: Our unfortunate first infection, patient zero — call him Marvin — is surrounded by 999 candidates for the next infection.

Marvin has contact with three people — Molly, Michael, and Martha — in the first day, and Mike and Molly catch the bug. Marvin goes on to have contact with three more people a day for the next four days, and two out of three of them also catch MARS-30, so at the end of his infectious period, Marvin has a total of 10 subsequent infections.

This is an epidemic. An infection that’s spreading rapidly in a population. Notice that doesn’t say anything about deaths: you can have an epidemic of something that doesn’t cause any deaths or even any noticeable sickness. The other words you hear bandied about are pandemic, which simply means an epidemic that’s widespread geographically. On the other end, you have an infection that’s endemic, which means there aren’t many new infections but the pathogen hasn’t gone away.

One of the ways we characterize an infectious disease is by the reproduction number R. R is the average number of new infections expected from a single case. What we’re seeing right now is that as of day 5, R for MARS-30 is roughly 10. I’m carefully avoiding talking about R₀ for reasons I’ll explain shortly.

So, anyway, Mike and Molly have their own five days — we’re up to day six now — and have infected their own 10 people. So at the end of that six days, we have 30 people infected by Marvin, Mike, and Molly. (And if you think I’m going to try to make up another 30 names starting with M you’re nuts.) We also have three people who have recovered and are therefore immune.

in the meantime, those other 30 people are infecting 10 more people each.

We can compute the actual number with some simple matrix multiplication — we’re actually integrating differential equations — but WordPress doesn’t show math well, and also people start to complain that “no one said there’d be math!” about the time you start integrating.

The point is that every day, lots more people are infected — and are no longer susceptible. They either have it and can’t catch it again, or they’ve recovered and can’t catch it again.

This means that as time goes on, the number of susceptible people decreases, which in turn means the chance that an infected person will come in contact with a susceptible person also decreases.

This is modeled by a compartmental model in which we have three compartments:

• Susceptible people
• Infected people
• Recovered people
• and we know that everyone is in one of those compartments

This is called an SIR model. Guess why? You may also see an SEIR model mentioned. That’s a compartmental model with four compartments: Susceptible, Exposed, Infected, and Recovered. The main difference is that SEIR models infections with an incubation period.

So, with this SIR model, at time t=0, there is one person, poor Marvin, in the Infected compartment, 999 people in the Susceptible compartment, and 0 people in the Recovered compartment. The next day, time t=1, there are three people in the Infected compartment, 997 people in the Susceptible compartment, and still no one in the Recovered compartment.

Day 2, and it’s 9 infected and 991 Susceptible.

As time passes, though, the number of infected and recovered people grows, and the number of susceptible people shrinks. On day 4, there are enough infected people that if an infected person meets three people, the chances are that at least one of them isn’t susceptible. By day 8, everyone has it or has had it. This is herd immunity.

If you keep track of the new infections each day, then you can easily compute the number of new infections per active infection. In this case, that starts around 2, but drops quickly. By day 6, it’s down to 1.8; on day 7, it’s 1.4; and the day after that, there are no new cases at all.

The Meaning of R₀

The average reproduction over the whole life of the MARS-30 epidemic is that each infection caused around 1.6 subsequent infections.

That’s an approximation of the famous R₀ — the expected number of subsequent infections following a single infection.

An SIR model actually defines a system of ordinary differential equations. In this case, there are two equations and two rates: the rate at which susceptible people get infected, and the rate at which infected people recover.

Given assumptions about those rates, you can integrate the differential equations and get a value for R₀ that’s independent of the size of the populations, although it’s still dependent on the actual number of initial infections and those assumed rates; that’s what people usually mean when they talk about R₀. This is also where the terminology gets sloppy: R₀ should be this computed and artificial number, which only changes if you change the initial conditions — the assumptions about the number infected and rates of infection and recovery. But people often talk about R₀ changing over time. What they really mean is R_t, the reproduction number at a particular time t, but that’s an OCD sort of thing. Most people will catch on to what you mean.

R₀ is useful because you can make some calculations based on it. The most important one is the herd immunity threshold: the proportion of the population that must be immune to lower the actual reproduction number below 1. A little algebra tells us that the herd immunity threshold is 1-(1/R₀).

In the artificial example of MARS-30, this is 1-(1/1.6), or around 38 percent. That means that once more than 38 percent of the population has gotten the bug, the number of new cases is going to start dropping: that’s what the herd immunity threshold means.

For real SARS-CoV-2, the estimated R₀ is between 2 and 3, the herd immunity threshold then is between 50 and 67 percent.

How many people in the U.S. are already immune?

We’re getting to the juicy stuff now. According to the CDC, about 131 million people in the U.S. are fully vaccinated and another 33 million have had the disease. So that’s a total of 164 million, or about 50 percent of the population. Now, remember that we know there are some people who appear to be naturally immune, and we also know that testing the population for antibodies shows a number of people have had the disease without knowing they had it. So, something over 50 percent of the population is now immune.

And that means?

With the basic reproduction number of SARS-CoV-2 being somewhere between 2 and 3, the herd immunity threshold is between 50 and 67 percent. So, we seem to be around the herd immunity threshold or have passed it.

What do we expect when we’re above the herd immunity threshold? The number of new cases starts to drop, and actually drops pretty quickly.

What are we seeing now? Sure enough, the number of new cases is dropping fast and has been dropping fast for quite a while. Here’s a chart from the CDC:

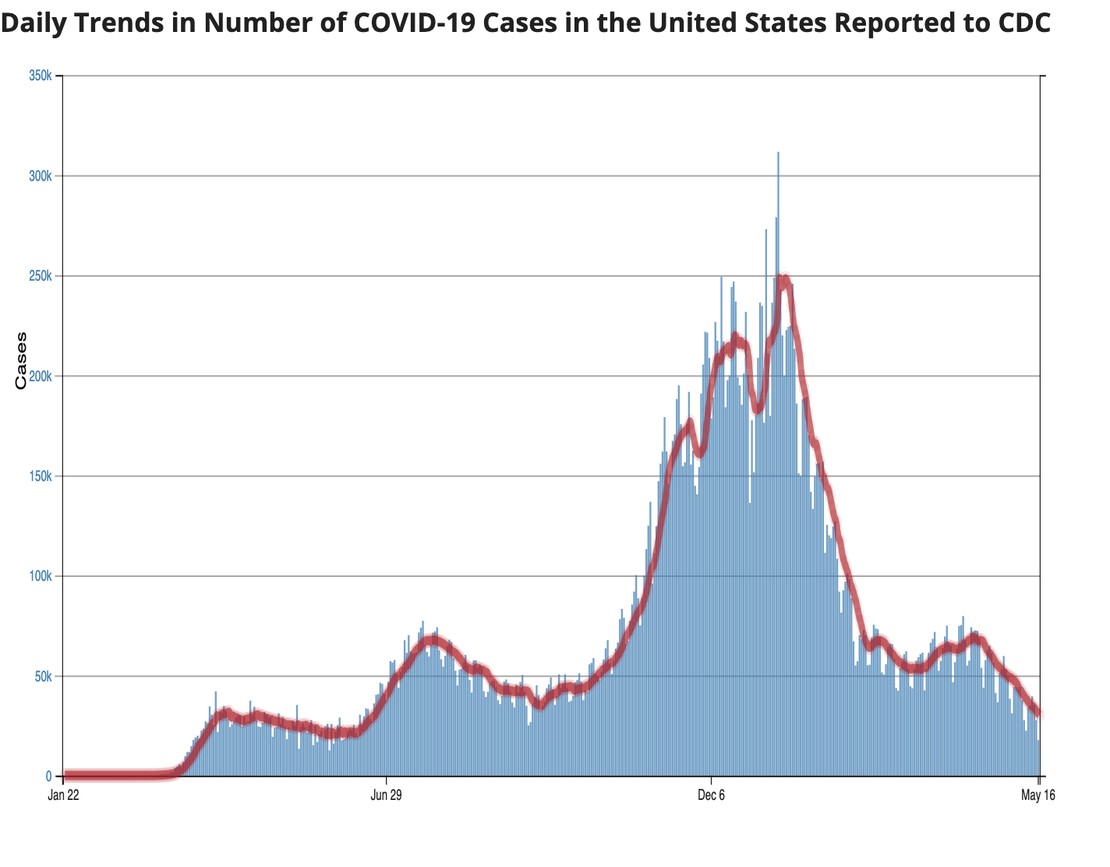
In other words, it looks very much like the U.S. is past the herd immunity threshold.

What this means.

The most important thing here is that this means the epidemic in the U.S. is probably over, or nearly over. (If R_t is something like 1.01, the epidemic isn’t over but the difference would be hard to see.) And if the epidemic is over, then epidemic emergency measures are no longer needed. It also means that readers should be very careful about some of the nonsense that’s coming out about it. For example, see this New York Times story from a few weeks ago:

Here’s what they said:

Now, more than half of adults in the United States have been inoculated with at least one dose of a vaccine. But daily vaccination rates are slipping, and there is widespread consensus among scientists and public health experts that the herd immunity threshold is not attainable — at least not in the foreseeable future, and perhaps not ever.

Instead, they are coming to the conclusion that rather than making a long-promised exit, the virus will most likely become a manageable threat that will continue to circulate in the United States for years to come, still causing hospitalizations and deaths but in much smaller numbers.

Think about our little toy Mars colony model: it actually reached herd immunity in a matter of days. Larger populations take longer, but what no one seems to be willing to say is that passing the herd immunity threshold is not just possible, it’s inevitable. It’s going to happen. Eventually, there will be too few susceptible people for the epidemic to continue. In the old days, before vaccines, polio, measles, chickenpox, and other things would get restarted as epidemics because people stubbornly insisted on having more babies, and the babies weren’t immune — so eventually there was a large population of susceptible people and the epidemic could start again. (Measles R₀ is estimated to be as high as 18, so the herd immunity threshold would be around 95 percent. Doesn’t take a lot of new babies to get back under 95 percent.)

The point is this: if someone tells you we’ll never reach the herd immunity threshold, or implies that we don’t have herd immunity until there are no new cases, they’re selling something.