It’s an old joke, or rather the framework for a whole bunch of old jokes, to start out saying “I’ve got good news and bad news.” So here’s a good one: I’ve got good news and bad news about the budget.
First the good news
None of the United States’ budget problems — not the deficit, not the national debt, not even the underfunding of Social Security and Medicare — is intrinsically insoluble, and I can prove it. It all comes from the magic of compound interest.
Compound interest is actually very easy to understand, although — as Euler, Napier, one of the Bernoullis, and every Calculus 101 student learned — the implications of compound interest are wide and varied indeed. But the basic idea is really simple.
Start with simple interest: if you have $100 in a savings account, and you get paid 5 percent simple interest, at the end of a year, your bank sends you a check for $5. Don’t spend it all in once place.
But now, let’s say you have $100 in a savings account paying 5 percent per year — which is called the principal amount — compounded. Now, the money the bank would have sent you by check in simple interest goes back into the account. After one year, you have $100 × 1.05, or $105. Leave your princely dividend in the account, and next year, you have $105 × 1.05 or $110.25, which is more than the simple interest computed on the principal amount alone. (Twenty-five cents more, in fact. Feel rich yet?) Wait another year, and you have $115.76; you’ve now made 76 cents more than you would have. Another year, it’s $121.55, or $1.55 more. If we lay that out in a table, you can see the differences. Every year the interest compounds, you make a little bit more than you would have from simple interest. But instead of a succession of little fussy numbers, let’s look at a picture:
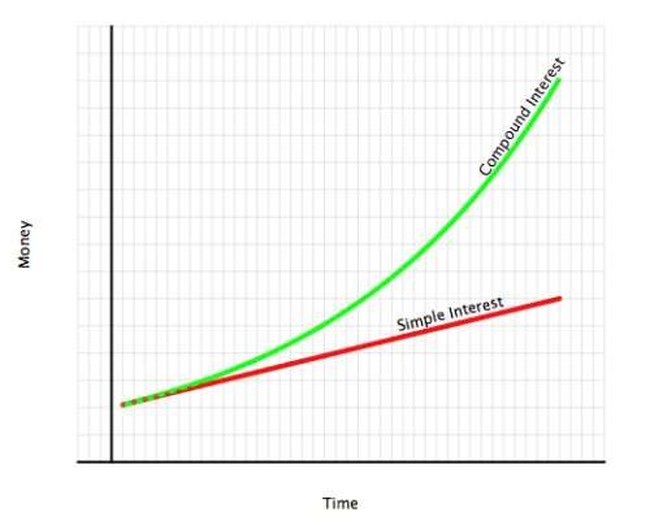
Over a long enough time, obviously, the compound interest is much more than the simple interest.
Now, thinking about something like this, we need to take into account inflation: over time, a dollar tends to buy less and less. That’s its own problem, but let’s avoid it this time: in this chart, and in all the rest of this article, we’re going to talk about inflation-adjusted dollars.
So now for a second topic. Taxes can be understood as money that comes in from the Gross Domestic Product or some other measure. (Old folks like me will remember when the important measure was called the Gross National Product. A little bit different in precise definition, but pretty much the same for our purposes.) The government, through various mechanisms, takes a cut off the top; this has a number of effects that we don’t need to think about right now; what’s important is that taxes are a percentage of the gross. If the GDP is X, then the total taxes will be some percentage of that — around .29 X in 1998. But the economy is growing, and since there’s no place for the extra to go that growth is compounding too.
In other words, if you leave everything alone, the amount of taxes collected grows and compounds too.
So now we’re ready for the good news: let’s assume that we start with current spending, and since we know there are a bunch of new programs being promised, like doggie treats, for electing the next government, we’ll assume that we actually assume spending of twenty-five percent more than current spending. We also assume that we leave the tax system completely alone; there are reasons you might want to raise them or lower them, but I don’t want to have that argument right now. So we just assume the tax system doesn’t change at all. The kicker is once we decide what the right spending level is — twenty-five percent isn’t magic; it could be any percentage — we leave it alone. From then on, we don’t let spending increase any faster than inflation, or in inflation-adjusted dollars, it stays constant. Then we get this picture:
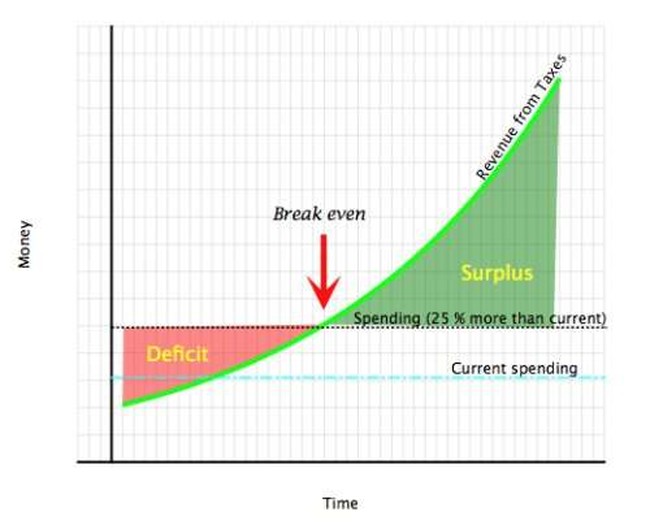
… which has a magic point at the big red arrow: the break-even point.
Or maybe you think that’s unrealistic, so let’s look at another chart. This time, we’re letting spending grow by some percentage every year, and still starting with the big spending increase of the last example. Then we get this chart:
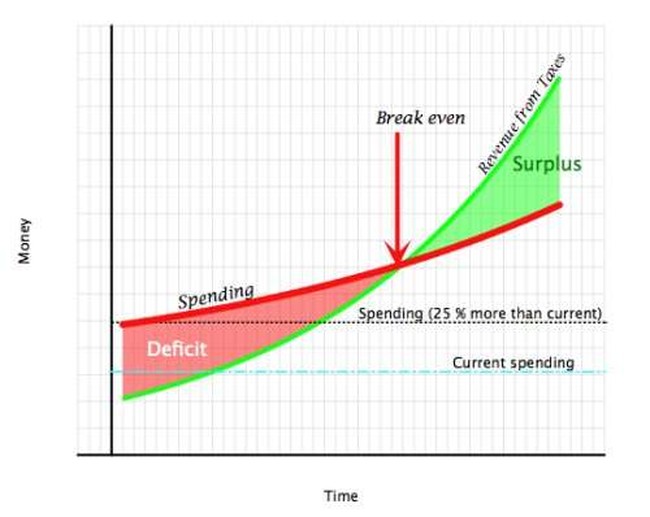
We can prove this all algebraically — I promise I won’t — but it comes down to this: if we can keep spending constant, or even just keep spending growing slower than the growth in GDP, even if we start at a major deficit, we will eventually break even and even start to accumulate a surplus. Keep that up long enough, and the debt goes away, the Social Security and Medicare underfunding goes away, and we can pay for all sorts of things. Or, better yet, give some of the money back so people can do what they want with it.
We know this is true, because this is exactly what happened in the 90s — the economy grew significantly faster than spending did. It’s not that spending didn’t grow, and in fact it grew faster than inflation; just not as fast as the economy did. Sure enough, in a few years, we had a budget surplus. Of course then we had a recession, which cut revenues temporarily, and a war, which raised spending, but that doesn’t actually matter: wherever you start, so long as spending isn’t growing as fast as the economy on average over a long time, you will eventually come back to a surplus.
Now for the Bad News
The bad news is, basically, that no one will tell you this. All politicians talk about the deficit — but that doesn’t stop each Congress member, from the rawest newly elected one to the speaker and the Senate leadership, from talking about the priority of their special project, which just coincidentally benefits their district and their big contributors. Add in entitlement programs, which seem to grow without bounds because there’s always someone — like AARP, not to name names — who wants to increase the spending on their particular group. The result is that government spending, over time, seems always to grow faster than the economy that supports it. Here’s a picture of that situation:
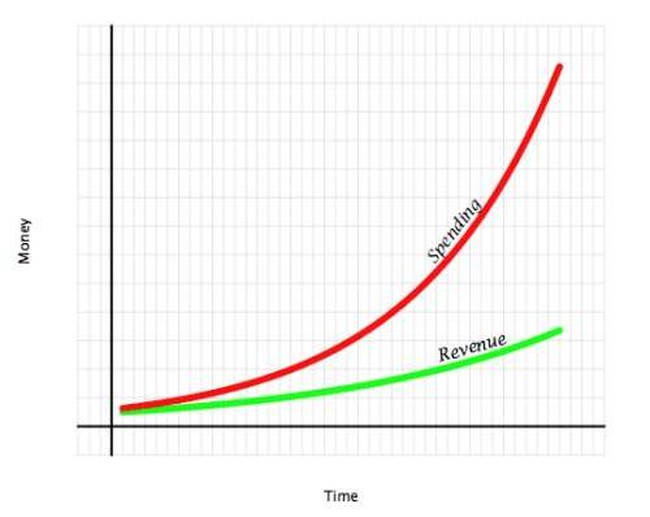
What’s more, no tax increase can keep this from happening. Tax the relatively few rich; you still can’t tax them more than 100 percent, and if spending grows faster than GDP, it will eventually overwhelm whatever taxes you can levy. Tax the many poor, and you get the same result — except you’ll be voted out of office first, because there are a lot more poor people than rich people. And it still won’t matter, because you cannot make revenues grow faster than the economy forever.
So the real bad news is that this is a mathematical fact: over the long term, government spending cannot grow faster than GDP forever. If you want more money for government programs, you eventually have to make sure the economy is growing faster than spending is. Of course, this has been a part of government programs since John Maynard Keynes: “In the long run, we’re all dead.” Many of the New Deal and Great Society programs depended, essentially, on the assumption that the people making the promises would be safely buried before the real costs came due.
If someone is trying to tell you something else, they either haven’t figured out the arithmetic, or they’re trying to put something over on you.










Join the conversation as a VIP Member